Day034 - 54. Spiral Matrix

54. Spiral Matrix

Given an m x n matrix, return all elements of the matrix in spiral order.

Example 1:

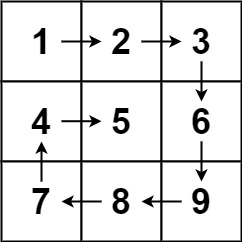
Input: matrix = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,2,3,6,9,8,7,4,5]

Example 2:

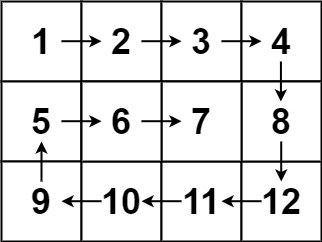
Input: matrix = [[1,2,3,4],[5,6,7,8],[9,10,11,12]]
Output: [1,2,3,4,8,12,11,10,9,5,6,7]

Constraints:

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 10
• -100 <= matrix[i][j] <= 100

내 풀이

class Solution:
    def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
        """
        matrix = [[1,2,3],
                  [4,5,6],
                  [7,8,9]]
        Output: [1,2,3,6,9,8,7,4,5]

        1. 자기자리 설정
        2. 자기 자리를 여기서 추가하고
        3. 추가한 자리를 X로 바꿈
        4. counter를 +1
        5. 다음 자리가 존재하는지 확인
            5-1 다음 자리가 존재하면
                5-1-1 다음 자리가 숫자라면
                    - pass
                5-1-2 다음 자리가 X라면
                    - move_idx를 하나 추가
            5-2 다음 자리가 존재하지 않으면
                - move_idx를 하나 추가
        6. move_idx를 기반으로 current_move 갱신
        7. r, c 포인터를 move기반 이동
        """   

        # 우, 하, 좌, 상 (row, col)
        move = [(0, 1), (1, 0), (0, -1), (-1, 0)]
        move_idx = 0
        current_move = move[0]

        r, c = 0, 0
        start = matrix[r][c]
        answer = []
        counter = 0

        while counter < len(sum(matrix, [])):    
            current_spot = matrix[r][c] 
            answer.append(current_spot)
            matrix[r][c] = "X"
            counter += 1
            try:
                next_spot = matrix[r + current_move[0]][c + current_move[1]]
                if next_spot == "X":
                    move_idx += 1
            except:
                move_idx += 1
            finally:
                current_move = move[move_idx%4]
                r += current_move[0]
                c += current_move[1]      
        
        return answer

# Time Complexity : \(O(N)\)